連載-“老朱陪您學Civil”之梁橋抗震4
2016-10-29 by:CAE仿真在線 來源:互聯網
連載-“老朱陪您學Civil”之梁橋抗震,你們的最愛-朱老師,小邁致力于與您分享一手技術資料,用技術創造幸福,你我一起!

3.Civil程序計算振型的三種方法
在一般的有限元分析中,由于系統的自由度很多,同時在研究系統的響應時,往往只需要了解少數較低的特征值及相應的特征向量,因此在有限元分析中,發展了一些適應上述特點而效率較高的解法(子空間迭代法、lanczos)。
midas Civil中除了提供精確的特征向量法分析外,還提供了與荷載相關的Ritz向量分析法。多重Ritz向量能用于線性和非線性結構的動力分析。與精確特征向量法相比,多重Ritz向量法用更少的時間可產生更精確的結果。
3.1子空間迭代法(wilson著作《結構靜力與動力分析》)
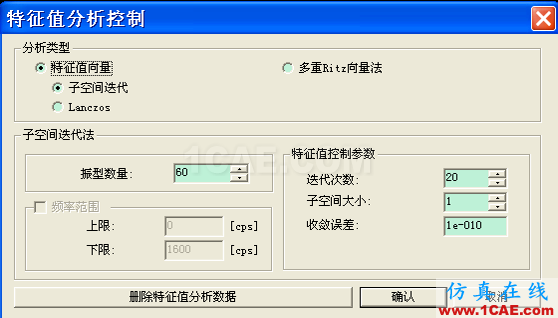
子空間迭代法是求解大型矩陣特征值問題的最常用最有效的方法之一,它適合于求解部分特征值解,被廣泛應用于結構動力學的有限元分析中。
子空間迭代法是假設r個起始向量(采用移頻法,通過特征值的移動和已收斂的特征向量的移出,使r保持在較小的數值,從而顯著提高計算效率和改進收斂速度)同時進行迭代(通過求解減縮廣義特征值問題)以求得矩陣的前p(<r)個特征值和特征向量。(如果r不是足夠大,一方面可能漏掉可能激起的振型;另一方面又可能引入不可能激起的振型)。
3.2 Lanczos方法
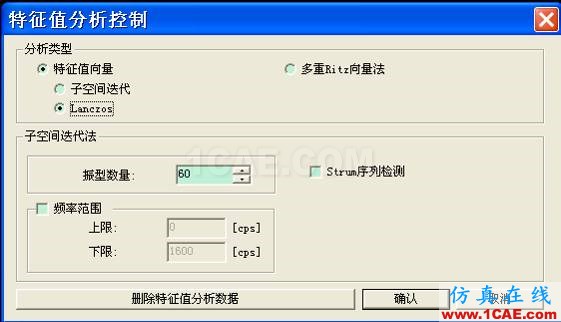
Lanczos方法和Ritz向量法的共同特點是直接生成一組Lanczos向量或者Ritz向量,對運動方程進行縮減,然后求解縮減了的運動方程的特征值問題,避免了迭代步驟(采用直接疊加法),從而具有更高的計算效率。
Lanczos法和Ritz向量法本質上一致,但是在實際計算中,由于計算機的截斷誤差和舍入誤差,導致數值上的不穩定性(例如虛假的多重特征值現象),因此妨礙了Lanczos方法的實際應用。20世紀70年代以后,很多研究工作者提出了不少Lanczos向量的重正交技術以調高其算法的穩定性,Ritz向量法從這個意義上說可以是這種,但由于他改變了成Lanczos向量的算法公式,導致以后求解的不是對角矩陣的特征值問題,而是一般矩陣特征值問題。
3.3多重Ritz向量法(求解的是一般矩陣特征值問題)
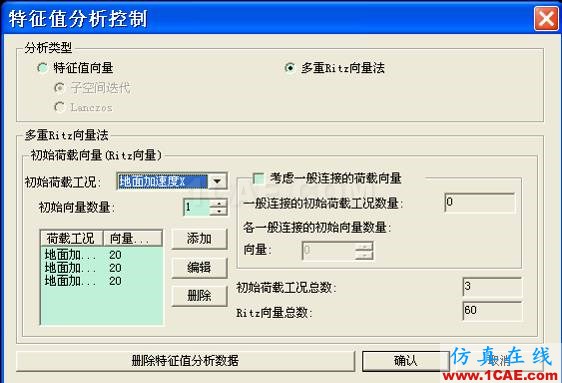
多重Ritz向量法認可結構動態響應是空間荷載分布的函數,考慮動力荷載的空間分布(當定義了初始向量后,第一個向量塊的靜態響應就來源于該初始荷載向量),可以避免漏掉可能激起的振型和引入不可能激起的振型,能夠顯著提高計算效率。
3.4 子空間迭代法、Lanczos法和多重Ritz向量法算例比較(荷載作用是對稱)
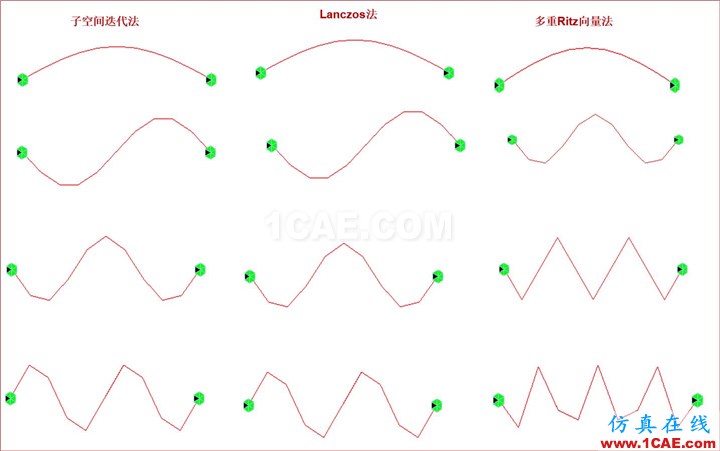
由圖可以清楚的發現:多重Ritz向量法和另外2種分析方法得到的振型圖是大不相同的。通過模態查看,可以發現多重Ritz向量法所有振型都是對稱的(荷載作用是對稱的),因為它考慮了空間荷載分布狀態及動力貢獻,所以他忽略了所有反對稱振型 。對于反對稱振型,并不是由荷載激發的,荷載在這些振型的動力貢獻為零。故:反應譜分析時較好的方法是采用多重Ritz向量法。
4.已知振型(模態)情況下如何計算反應譜下的結構受力情況
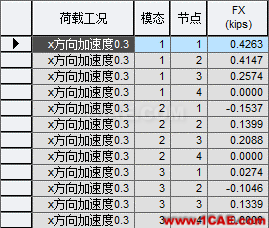
4.1單振型施加慣性力的方法

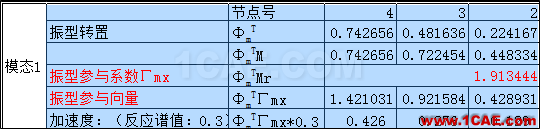
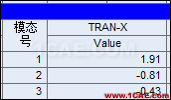
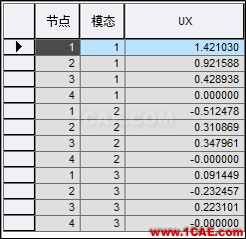
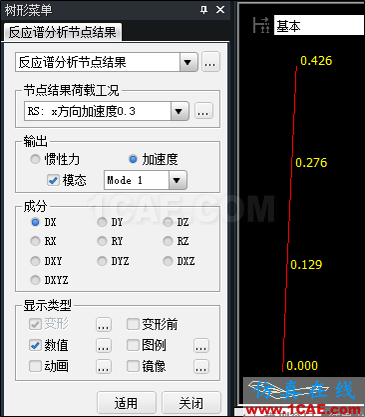
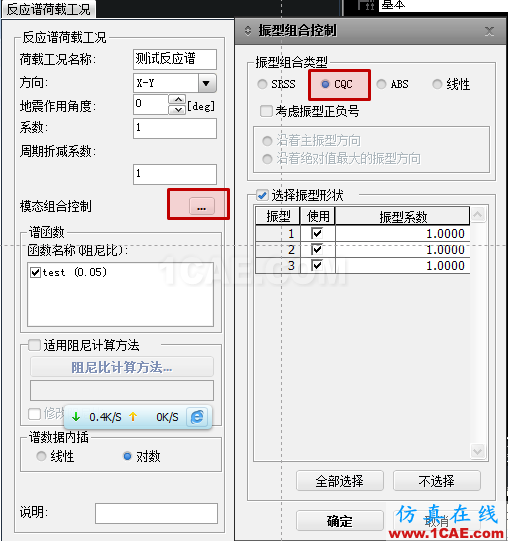
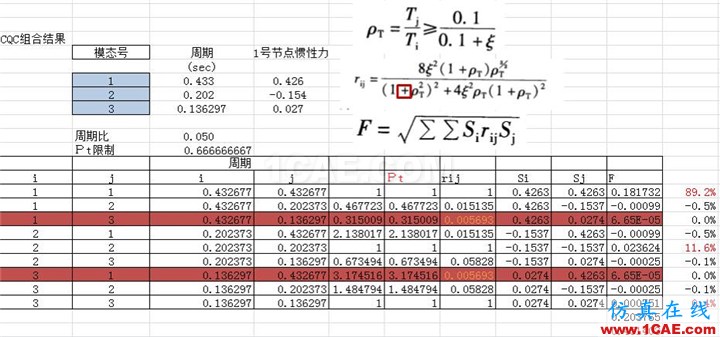
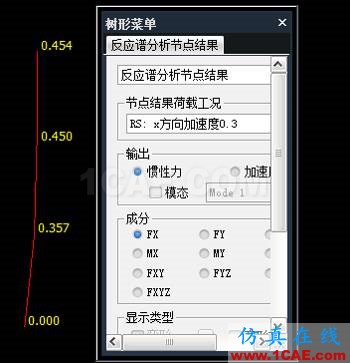
4.2各振型的組合結果


*連載-每周更新,敬請期待,也可留言向朱老師提問
相關標簽搜索:連載-“老朱陪您學Civil”之梁橋抗震4 Midas Civil分析 Midas Civil培訓 Midas Civil培訓課程 Midas Civil在線視頻教程 Midas Civil技術學習教程 Midas Civil軟件教程 Midas Civil資料下載 Midas Civil代做 Midas Civil基礎知識 Fluent、CFX流體分析 HFSS電磁分析 Ansys培訓






