梁單元-有限元分析
2017-04-08 by:CAE仿真在線 來源:互聯網
有限元法的基本思想是將結構離散化,用有限個容易分析的單元來表示復雜的對象,單元之間通過有限個節點相互連接,然后根據變形協調條件綜合求解。由于單元的數目是有限的,節點的數目也是有限的,所以稱為有限元法(FEM,Finite Element Method)。是隨著電子計算機的發展而迅速發展起來的一種彈性力學問題的數值求解方法。
有限元法是最重要的工程分析技術之一。它廣泛應用于彈塑性力學、斷裂力學、流體力學、熱傳導等領域。有限元法是60年代以來發展起來的新的數值計算方法,是計算機時代的產物。雖然有限元的概念早在40年代就有人提出,但由于當時計算機尚未出現,它并未受到人們的重視。
隨著計算機技術的發展,有限元法在各個工程領域中不斷得到深入應用,現已遍及宇航工業、核工業、機電、化工、建筑、海洋等工業,是機械產品動、靜、熱特性分析的重要手段。早在70年代初期就有人給出結論:有限元法在產品結構設計中的應用,使機電產品設計產生革命性的變化,理論設計代替了經驗類比設計。目前,有限元法仍在不斷發展,理論上不斷完善,各種有限元分析程序包的功能越來越強大,使用越來越方便。
所謂梁桿結構是指其長度比橫截面尺寸大很多的梁和桿件、以及由它們組成的系統,這一類結構的應力、應變和位移都是一個坐標的函數,所以屬于一維單元問題。
特點:桿件位于一個平面內,桿件間用鉸節點連接,作用力也在該平面內。
單元特性:只承受拉力或壓力。
單元劃分:常采用自然單元劃分。即以兩個鉸接點之間的桿件作為一個單元。為使桁架桿件只產生軸力,桁架的計算常作以下假定:
①桁架中每根桿件的兩端由理想鉸聯結;
②每根桿件的軸線必須是直線;
③所有桿件的軸線都只交于所聯理想鉸的幾何中心。
④荷載均只作用于理想鉸的幾何中心。
在此條件下所算得的各種應力稱為主應力。實際上各種桁架結構不可能完全滿足上述各假定,因而桿件將產生彎曲,由這種彎曲而在桿件中所引起的軸向應力稱為次應力。鋼桁架如設計得較合理,次應力一般不太大;鋼筋混凝土或預應力混凝土桁架,由于其結點剛度大、桿件粗短,次應力的影響不能忽視。
特點:與平面桁架的不同在于桿件之間以剛性鉸接點作為連接。
單元特性:除承受拉、壓軸向載荷外,還要承受剪力和彎矩。
單元劃分:除采用自然單元劃分外。即以兩個剛接點之間的桿件作為一個單元。同時也要考慮在集中載荷作用位置、截面突變位置和分布載荷突變的位置增設節點。
多用鋼筋混凝土或鋼材建造,剛架結構多為空間剛架,但許多空間剛架可分解為平面剛架進行計算。剛架可分為靜定剛架和超靜定剛架,但工程中所應用的主要是超靜定剛架。
特點:簡化了的剛架。
特性:不考慮軸向變形,只考慮垂直于軸線的線位移和軸線平面內的轉角位移。
單元劃分:同剛架。
A.粱在變形前垂直于粱軸線的橫截面,變形后仍然為平面(剛性橫截面假定);
B.橫截面變形后的平面仍與變形后的軸線相互垂直。
也就是說歐拉梁忽略了剪切變形和轉動慣量,認為初始垂直于中性軸的截平面在變形時仍保持為平面垂直于中性軸(Kirchhoff假設),即認為截面的轉動等于撓度曲線切線的斜率。適用于梁的高度遠小于跨度情況下。
A.粱在變形前垂直于粱軸線的橫截面,變形后仍然為平面(剛性橫截面假定);
B.由于歐拉-伯努利梁的第二個假設忽略了梁的剪切變形,對于有效長度較短或復合材料梁板橋時,忽略剪切變形是不妥的,鐵木辛柯提出讓梁的應力應變關系得到滿足,即考慮剪切變形與轉動慣量。
在鐵木辛柯梁中,需要考慮橫向剪切變形影響的情況,如高度相對跨度不太小的高梁。此時梁內的橫向剪切力Q所產生的剪切變形將引起梁的附加撓度,并使原來垂直于中性面的截面變形后不再與中性面垂直,且發生翹曲。
節點位移向量
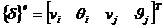
(1-1)
節點力向量
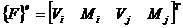
(1-2)
每個單元四個自由度,所以可以有4個待定系數
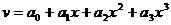
(1-3)
有材料力學知,撓度與轉角之間的關系是:
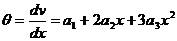
(1-4)
將i、j節點的位移代入,求得待定系數:

(1-5)
所以
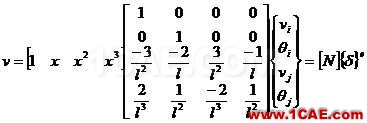
(1-6)
其中[N]為形函數矩陣
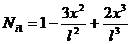
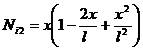
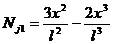
(1-7)
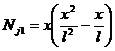
它也滿足前面形函數的性質。
梁彎曲變形時,若忽略剪切的影響,由材料力學知道:
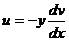
(1-8)
將它代入到幾何方程,得:
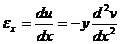
(1-9)
換入位移插值公式
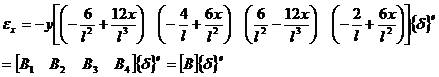
(1-10)
單向應力狀態,所以
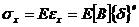
(1-11)
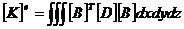
(1-12)
代入[B]矩陣和[D]=E,并考慮
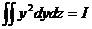
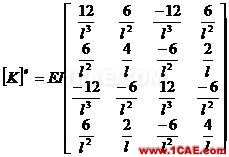
(1-13)
其中:
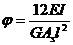
——剪切影響系數,As為有效的抗剪切面積。
有一外伸梁及其承載情況如圖所示,其中,
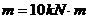
,
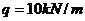
,
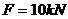
。對該梁進行分析,畫出彎矩圖和剪力圖。
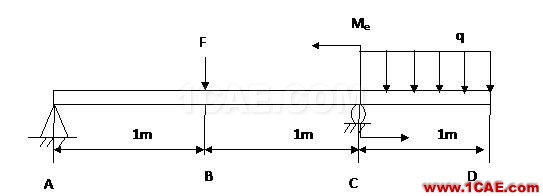
圖1. 外伸梁結構示意圖
用材料力學計算所得剪力和彎矩圖如下(以供對照):
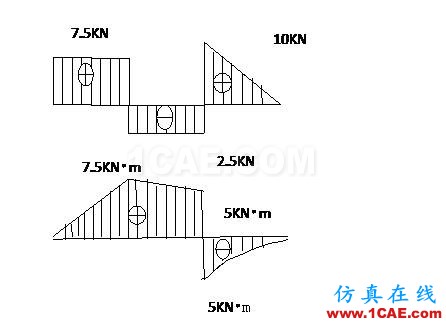
圖2. 外伸梁的剪力圖和彎矩圖
利用有限元軟件ANSYS對此外伸梁及其承載情況進行分析。
步驟概括:
1)創建梁的各個節點;
2)顯示各個節點。
2.定義單元類型和材料
1)定義單元類型-2D elastic 3;
2)定義材料特性- Isotropic, 在EX后的文本框內輸入數值207e5作為彈性模量;
3)定義幾何參數。
1)創建單元;
2)顯示單元資料。
1)施加集中載荷F;
2)施加彎矩M;
3)施加分布載荷q。
1)改變分析類型;
2)求解。
1)顯示梁單元變形結果;
2)建立元素結果表:
①創建單元表,計算節點彎矩;
②創建單元表,計算節點剪力。
3)列出所有表格資料:
①列出資料;
②畫剪力圖;

圖3. 外伸梁的剪力圖
③畫彎矩圖。

圖4. 外伸梁的彎矩圖
將理論的彎矩圖和剪力圖與ansys軟件分析出的結果是一致的,通過對比,我們可以看出有限元的優越性。
相關標簽搜索:梁單元-有限元分析 Ansys有限元培訓 Ansys workbench培訓 ansys視頻教程 ansys workbench教程 ansys APDL經典教程 ansys資料下載 ansys技術咨詢 ansys基礎知識 ansys代做 Fluent、CFX流體分析 HFSS電磁分析 Abaqus培訓






