各種模態分析方法總結與比較
2017-05-08 by:CAE仿真在線 來源:互聯網
模態分析是計算或試驗分析固有頻率、阻尼比和模態振型這些模態參數的過程。
模態分析的理論經典定義:將線性定常系統振動微分方程組中的物理坐標變換為模態坐標,使方程組解耦,成為一組以模態坐標及模態參數描述的獨立方程,以便求出系統的模態參數。坐標變換的變換矩陣為模態矩陣,其每列為模態振型。
模態分析是研究結構動力特性一種近代方法,是系統辨別方法在工程振動領域中的應用。模態是機械結構的固有振動特性,每一個模態具有特定的固有頻率、阻尼比和模態振型。這些模態參數可以由計算或試驗分析取得,這樣一個計算或試驗分析過程稱為模態分析。這個分析過程如果是由有限元計算的方法取得的,則稱為計算模記分析;如果通過試驗將采集的系統輸入與輸出信號經過參數識別獲得模態參數,稱為試驗模態分析。通常,模態分析都是指試驗模態分析。振動模態是彈性結構的固有的、整體的特性。如果通過模態分析方法搞清楚了結構物在某一易受影響的頻率范圍內各階主要模態的特性,就可能預言結構在此頻段內在外部或內部各種振源作用下實際振動響應。因此,模態分析是結構動態設計及設備的故障診斷的重要方法。
模態分析最終目標是在識別出系統的模態參數,為結構系統的振動特性分析、振動故障診斷和預報以及結構動力特性的優化設計提供依據。
(一)單自由度法
一般來說,一個系統的動態響應是它的若干階模態振型的疊加。但是如果假定在給定的頻帶內只有一個模態是重要的,那么該模態的參數可以單獨確定。以這個假定為根據的模態參數識別方法叫做單自由度(SDOF)法n1。在給定的頻帶范圍內,結構的動態特性的時域表達表示近似為:
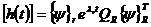 2-1
2-1
而頻域表示則近似為:
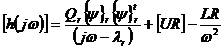 2-2
2-2
單自由度系統是一種很快速的方法,幾乎不需要什么計算時間和計算機內存。
這種單自由度的假定只有當系統的各階模態能夠很好解耦時才是正確的。然而實際情況通常并不是這樣的,所以就需要用包含若干模態的模型對測得的數據進行近似,同時識別這些參數的模態,就是所謂的多自由度(MDOF)法。
單自由度算法運算速度很快,幾乎不需要什么計算和計算機內存,因此在當前小型二通道或四通道傅立葉分析儀中,都把這種方法做成內置選項。然而隨著計算機的發展,內存不斷擴大,計算速度越來越快,在大多數實際應用中,單自由度方法已經讓位給更加復雜的多自由度方法。
1、峰值檢測
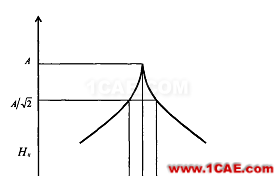
峰值檢測是一種單自由度方法,它是頻域中的模態模型為根據對系統極點進行局部估計(固有頻率和阻尼)。峰值檢測方法基于這樣的事實:在固有頻率附近,頻響函數通過自己的極值,此時其實部為零(同相部分最小),而虛部和幅值最大(相移達90°,幅度達峰值)圖1。出現極值的那個固有頻率就是阻尼固有頻率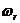 的良好估計。相應的阻尼比
的良好估計。相應的阻尼比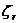 ,的估計可用半功率點法得到。設
,的估計可用半功率點法得到。設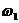 和
和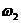 分處在阻尼固有頻率的兩側(
分處在阻尼固有頻率的兩側(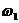 <
<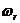 <
<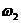 ),則:
),則:
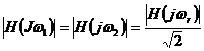 2-3
2-3
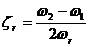 2-4
2-4
2、模態檢測
模態檢測是根據頻域中的模態模型對復模態(或實模態)向量進行局部估計的一種單自由度方法。在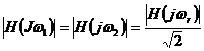 中略去剩余項則單個頻響函數在
中略去剩余項則單個頻響函數在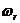 處的值近似為:
處的值近似為:
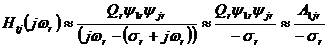 2-5
2-5
由此式可見,頻響函數在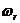 處的值乘以模態阻尼因
處的值乘以模態阻尼因
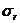 ,就是留數(的估計值如圖1。利用這種模態檢測方法之前,先要估計出
,就是留數(的估計值如圖1。利用這種模態檢測方法之前,先要估計出
3、圓擬合
圓擬合是一種單自由度方法,用頻域中的模態模型對系統極點和復模態(或實模態)向量進行局部估計。此方法依據事實是:單自由度系統的速度頻響函數(速度對力)在奈奎斯特圖(即實部對虛部)上呈現為一個圓。如果把其他模態的影響近似為一個復常數,那么在共振頻率 附近,頻響函數的基本公式為:
附近,頻響函數的基本公式為:
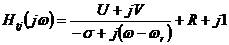 2-6
2-6
因此,首先要選擇共振頻率附近的一組頻率響應點,通過這些點擬合成一個圓。阻尼固有頻率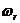 可以看成是復平面上數據點之間角度變化率最大(角間隔最大)的那個點的頻率,也可以看成是相位角與圓心的相位角最為接近的那個數據點的頻率。對于分得開的模態而言,二者的差別是很小。
可以看成是復平面上數據點之間角度變化率最大(角間隔最大)的那個點的頻率,也可以看成是相位角與圓心的相位角最為接近的那個數據點的頻率。對于分得開的模態而言,二者的差別是很小。
阻尼比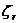 估計如下:
估計如下:
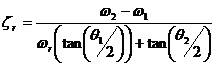 2-7
2-7
式中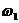 ,
,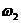 :分居在
:分居在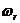 兩側的兩個頻率點:
兩側的兩個頻率點: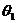 ,
,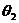 :分別為頻率點在
:分別為頻率點在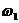 和
和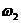 得半徑與
得半徑與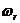 得半徑之間的夾角。
得半徑之間的夾角。
圓的直徑和阻尼固有頻率點的角位置含有復留數U+jV的信息:
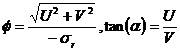 2-8
2-8
式中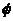 :圓的直徑
:圓的直徑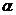 :園心與固有頻率點的連線跟虛軸之間的夾角.
:園心與固有頻率點的連線跟虛軸之間的夾角.
圓擬合法速度也很快,但為避免結果出錯,特別是在模態節點附近,需要操作者參與。
(二)單自由度與多自由度系統
粘性阻尼單自由度SDOF系統如圖2的力平衡方程式表示慣性力、阻尼力、彈性力與外力之間的平衡。
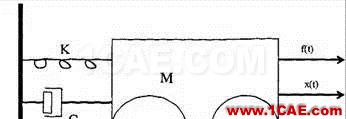
圖2 單自由度系統
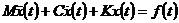 2-9
2-9
其中M:質量C: 阻尼K: :加速度,速度,位移 f:外力 t時間變量,把結構中所呈現出來的全部阻尼都近似為一般的粘性阻尼。
:加速度,速度,位移 f:外力 t時間變量,把結構中所呈現出來的全部阻尼都近似為一般的粘性阻尼。
把上面的時間域方程變換到拉氏域復變量P,并假設初始位移和初始速度為零,則得到拉氏域方程:
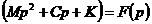 ,或
,或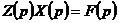 Z:動剛度經過變換可得傳遞函數的定義,
Z:動剛度經過變換可得傳遞函數的定義,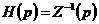 即
即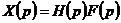
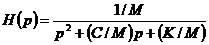 2-10
2-10
上式右端的分母叫做系統特征方程,它的根即是系統的極點是:
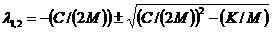 2-11
2-11
如果沒有阻尼C=0,則所論系統是保守系統。我們定義系統的無阻尼固有頻率為:
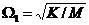 2-4
2-4
臨界阻尼Cc的定義為使(2.3)式中根式項等于零的阻尼值:
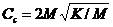 2-5
2-5
而臨界阻尼分數或阻尼比ζ1為:ζ1=CCc,阻尼有時也有用品質因數即Q因數表示:
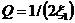 2-6
2-6
系統按阻尼值的大小可以分成過阻尼系統(ζ1>1)、臨界阻尼系統(ζ1=1)和欠阻尼系統(ζ1<1)。過阻尼系統的響應只含有衰減成分、沒有振蕩趨勢。欠阻尼系統的響應時一種衰減振動,而臨界阻尼系統則是過阻尼系統與欠阻尼系統之間的一種分界。
實際系統的阻尼比很少有大于10%的,除非這些系統含有很強的阻尼機制,因此我們只研究欠阻尼的情形。
在欠阻尼的情況下式2-11兩個共軛復根:
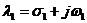 ,
,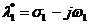 2-7
2-7
其中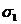 為阻尼因子
為阻尼因子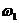 為阻尼固有頻率。有關系統極點的另外一些關系式有:
為阻尼固有頻率。有關系統極點的另外一些關系式有:
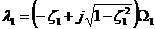 2-8
2-8
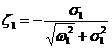 2-9
2-9
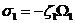 2-10
2-10
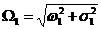 2-11
2-11
2-2式寫成 如下形式:
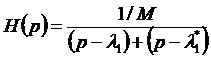 2-12
2-12
在展開成部分分式形式,則有:
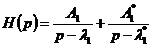 ,這里
,這里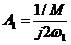 2-13
2-13
這里的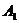 和
和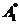 是留數。
是留數。
多自由度系統
多自由度系統可以用簡單的力平衡代數方程演化成形式相似的一個矩陣的方程。下面是以而自由度系統為例。如圖:
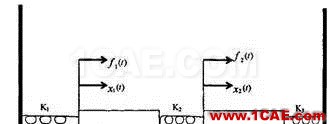
圖3 多自由度系統
該系統的運動方程如下:
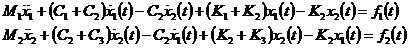 2-14
2-14
寫成矩陣形式是
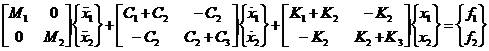 2-15
2-15
或者
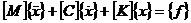 2-16
2-16
其中[M]、[C]、[K]、{f(t)}和{x(t)}分別為質量矩陣、阻尼矩陣、剛度矩陣、方向量和響應向量。把這個時間域的矩陣方程變換到拉氏域(變量為p)且假定初始位移和初始速度為零,則得:
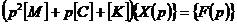 2-17
2-17
或者是
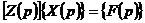 式中:[Z(p)]動剛度矩陣 2-18
式中:[Z(p)]動剛度矩陣 2-18
可以得到傳遞函數矩陣為:
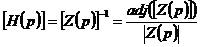 2-19
2-19
式中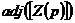 :
: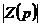 的伴隨矩陣,等于
的伴隨矩陣,等于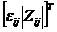 ;
;
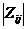 :
: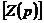 去掉第行第列后的行列式
去掉第行第列后的行列式
 ;
;
傳遞函數矩陣含有幅值函數。
2-19式中的分母,即是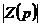 的韓烈士,叫做系統的特征方程。與單自由度情況一樣,系統特征方程的根,即系統極點,決定系統的共振頻率。根據特征值問題,可以求出系統特征方恒的根。為了把系統方程2-17轉化為一般的特征值問題公式,加入下面的恒等式:
的韓烈士,叫做系統的特征方程。與單自由度情況一樣,系統特征方程的根,即系統極點,決定系統的共振頻率。根據特征值問題,可以求出系統特征方恒的根。為了把系統方程2-17轉化為一般的特征值問題公式,加入下面的恒等式:
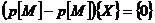 2-20
2-20
將此式與2-17式結合在一起得:
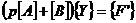 2-21
2-21
其中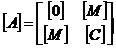 ,
,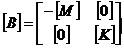 ,
,
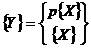 ,
,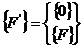 。
。
如果力函數等于零,那么式2-19就成了關于實值矩陣的一般特征值問題,其特征值馬祖下列方程的p值:
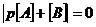 2-22
2-22
它的根就是特征方程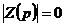 的根。對于N各自由度系統,此方程有2N個呈復共軛對出現的特征根:
的根。對于N各自由度系統,此方程有2N個呈復共軛對出現的特征根:
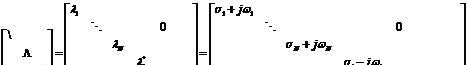 2-23
2-23
同單自由度系統一樣,多自由度系統的極點的實部是阻尼因子,虛部是阻尼固有頻率。
(三)實模態和復模態
按照模態參數(主要指模態頻率及模態向量)是實數還是復數,模態可以分為實模態和復模態。對于無阻尼或比例阻尼振動系統,其各點的振動相位差為零或180度,其模態系數是實數,此時為實模態;對于非比例阻尼振動系統,各點除了振幅不同外相位差也不一定為零或180度,這樣模態系數就是復數,即形成復模態。
1 復模態與實模態理論
在擬合頻段, 實模態理論中傳遞函數在 k點激勵 Z 點響應的留數表達式為
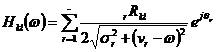
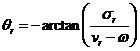
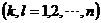 (1)
(1)
其中,
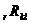 為留數;
為留數;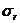 和
和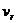 構成的復數為系統的復特征值
構成的復數為系統的復特征值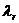 :
: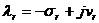 擬合頻段復模態理論中傳遞函數在 k點激勵 f 點響應的留數表達式為
擬合頻段復模態理論中傳遞函數在 k點激勵 f 點響應的留數表達式為
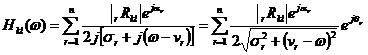
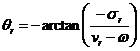
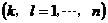 (2)
(2)
由(1)、(2)式中可以看出,傳遞函數共振峰處復模態的相位與實模態相位的差別在于多出的復留數相位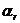 ,由傳遞函數的逆變換可以得到脈沖響應函數,由此可以得到物理坐標系中結構的自由響應表達式。
,由傳遞函數的逆變換可以得到脈沖響應函數,由此可以得到物理坐標系中結構的自由響應表達式。
對于無阻尼結構,t時刻第r階模態k點的振動為
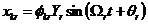 (3)
(3)
粘性比例阻尼:t時刻第r階模態k點的振動為
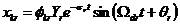 (4)
(4)
一般粘性阻尼:t時刻第r階模態k點的振動為
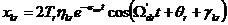 (5)
(5)
式中,φkr表示振型幅值;Ω表示模態頻率;θ表示相位角。
可以看出, 無阻尼和比例阻尼系統的初相位與初始條件有關,與物理坐標無關, 具有模態( 振型) 保持性; 而一般粘性阻尼系統的初相位還與物理坐標 k 有關, 每個物理坐標振動時并不同時達到平衡位置和最大位置, 不具備模態保持性, 是行波形式.但各物理坐標的相位差保持不變, 各點的振動周期、 衰減率仍保持相同 J .從物理坐標點的自由響應公式還可看出, 即使各測點留數為復數, 但如果留數的相位差, 即振型的幅角相同, 那么還是可以得到振動周期內形狀不變且節點固定的振型.這樣模態雖是復模態, 但表現出實模態的性質.因此實模態理論的實振型與復模態理論中復模態的差別在于各測點峰值相位差的大小.
2 實模態提取方法
復模態理論中模態參數( 特征值和特征向量)均為復數, 在進行結構模型修正時大量采用復數矩陣和復數迭代運算,計算工作量大,效率低;實模態理論中模態參數為實數,物理概念明確,后續結構模型修正計算公式簡單,計算工作量小又節約空間,故實模態得到廣泛的應用,實際測試得到的傳遞函數留數一般都為復數,要由復模態經過實模態提取技術才能得到實模態。復模態提取實模態的方法主要有:根據復模態的實部、虛部或相位確定實模態的傳統方法;I b r a h i m的 擴大模型法; C h e n的傳遞函數提取法等。目前的模態分析軟件中普遍使用的為傳統方法。由復模態實部或虛部獲得實模態向量的方法為:直接取復留數的實部或虛部作為實模態理論中的留數,進行規格化得到實模態振型.
由復模態相位獲得實模態向量的方法為: 取復留數的幅值作為實模態理論中的留數, 根據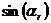 的數值接近1或-1,將留數相位歸為90 °或-90 °,然后盡享振型規格化,得到實模態振型,此振型中各測點相位差即為0 °或180 °。用復模態理論獲得的復模態向量,由復振型的周期變化中t=0即振動達到最大幅度時的振幅之比表示。
的數值接近1或-1,將留數相位歸為90 °或-90 °,然后盡享振型規格化,得到實模態振型,此振型中各測點相位差即為0 °或180 °。用復模態理論獲得的復模態向量,由復振型的周期變化中t=0即振動達到最大幅度時的振幅之比表示。
三、模態分析的應用與發展
模態分析技術的應用可歸結為以下幾個方面:
1) 評價現有結構系統的動態特性;
2) 在新產品設計中進行結構動態特性的預估和優化設計;
3) 診斷及預報結構系統的故障;
4) 控制結構的輻射噪聲;
5) 識別結構系統的載荷。
對于實際的工程,用有限元軟件分析需要的頻率段,可查找振動原因,或校核。模態分析可以看出在那些頻率段需要防止或避免共振時很有用。
首先,頻率和振型是結構的固有特性,任何結構都可以進行模態分析;其次,結構的功能是不同的,不同結構對應的模態分析的用途是有差別的。對建筑結構,模態分析可以知道結構的避頻設計、用于抗震設計計算以及考慮動力荷載的放大作用等。另外,還可以挖掘振型有關的信息。
機器、建筑物、航天航空飛行器、船舶、汽車等的實際振動千姿百態、瞬息變化。模態分析提供了研究各種實際結構振動的一條有效途徑。
首先,將結構物在靜止狀態下進行人為激振,通過測量激振力與胯動響應并進行雙通道快速傅里葉變換(FFT)分析,得到任意兩點之間的機械導納函數(傳遞函數)。用模態分析理論通過對試驗導納函數的曲線擬合,識別出結構物的模態參數,從而建立起結構物的模態模型。根據模態疊加原理,在已知各種載荷時間歷程的情況下,就可以預言結構物的實際振動的響應歷程或響應譜。
模態分析軟件以美國的ME’ScopeVES的功能最為全面。ME’ScopeVES軟件的功能包括信號處理(signal Process ing)、運行撓曲振型(OperatingDeflection Shapes)、模態分析(Modal Analysi s)、結構改正(SDM)和聲學分析(Acoustics Analysi S)等,解決和分析機器與結構的振動噪聲問題。
主要可用于:
1、可以顯示被測物體的實際工作形態(0DS)、模態、聲學分布形態和工程數據的形態等;
2、模塊化結構便于用戶根據自己的需要選擇合適的產品;
3、強大的圖形顯示、結構編輯、數據處理及動畫顯示功能;
4、軟件的開放性好,能夠與全球的多家廠商的硬件兼容;
5、主要應用的領域:航空航天、建筑橋梁、汽車制造、鋼鐵冶金、軍工裝備等。
模態分析與參數辨識作為結構動力學中的一種逆問題分析方法并在工程實踐中應用是從60年代中、后期開始,至今已有近四十年的歷史了。這一技術首先在航空、宇航及汽車工業中開始發展。由于電子技術、信號處理技術與設備的發展,到80年代末這項技術已成為工程中解決結構動態性能分析、振動與噪聲控制、故障診斷等問題的重要工具。目前這一技術已漸趨成熟。經過二十余年的研究發展,到目前為止模態分析技術已在我國各個工程領域中廣泛應用,成為一種解決工程問題的重要手段。
在工程應用方面模態分析已滲透到我國各個工程領域,并取得了不少成就。例如,某型火箭全裝置的實物模態試驗保證了火箭的準確發射與導航,防止了發射的失敗;模態分析與參數識別技術曾被成功地用于解決某型航空發動機的嚴重振動故障,取得重大經濟及社會效益;某型魚雷全裝置實物水下模態試驗為魚雷的振動與噪聲控制確保導航性能提供了技術依據;遠東第一高塔的上海東方明珠電視塔的振動模態試驗,為高塔的抗風抗地震安全性設計提供了技術依據;目前世界上跨度第一的斜拉索楊浦大橋的振動試驗對大橋抗風振動的安全性分析與故障診斷提供了技術依據;建立在模態分析技術上的樁基斷裂檢測技術已在高層建筑施工中廣泛應用,提高了樁基的質量,確保高層建筑的安全;……等等,這些成就不勝枚舉。總之,二十余年的發展是迅速的,成就是顯著的,回顧這一發展過程和取得的成就,可更激勵我們朝著新的目標奮發前進。
模態分析技術發展到今天已趨成熟,特別是線性模態理論方面的研究已日臻完善,但在工程應用方面還有不少工作可做。首先是如何提高模態分析的精度,擴大應用范圍。增加模態分析的信息量是提高分析精度的關鍵,單靠增加傳感器的測點數目很難實現,目前提出的一種激光掃描方法是大大增加測點數的有效辦法,測點數目的增加隨之而來的是增大數據采集與分析系統的容量及提高分析處理速度,在測試方法、數據采集與分析方面還有不少研究工作可做。對復雜結構空間模態的測量分析、頻響函數的耦合、高頻模態檢測、抗噪聲干擾……等等方面的研究尚需進一步開展。
模態分析當前的一個重要發展趨勢是由線性向非線性問題方向發展。非線性模態的概念早在1960年就由Rosenberg提出,雖有不少學者對非線性模態理論進行了研究,但由于非線性問題本身的復雜性及當時工程實踐中的非線性問題并引引起重視,非線性模態分析的發展受到限制。近年來在工程中的非線性問題日益突出,因此非線性模態分析亦日益受到人們的重視。最近已逐步形成了所謂非線性模態動力學。
關于非線性模態的正交性、解耦性、穩定性、模態的分叉、滲透等問題是當前研究的重點。在非線性建模理論與參數辨識方面的研究工作亦是當今研究的熱點。非線性系統物理參數的識別、載荷識別方面的研究亦已開始。展望未來,模態分析與試驗技術仍將以新的速度,新的內容向前發展。
綜合自網絡
相關標簽搜索:各種模態分析方法總結與比較 Ansys有限元培訓 Ansys workbench培訓 ansys視頻教程 ansys workbench教程 ansys APDL經典教程 ansys資料下載 ansys技術咨詢 ansys基礎知識 ansys代做 Fluent、CFX流體分析 HFSS電磁分析 Abaqus培訓






