Isight梯度優(yōu)化算法淺析

2016-10-24 by:CAE仿真在線來源:互聯(lián)網(wǎng)

梯度算法通過在設計空間中的當前位置設定一個前進方法和搜索步長從而獲得設計空間中的另一個位置,并判斷收斂性。Isight中梯度優(yōu)化算法有三種NLPQL,LSGRG和MMFD,這里通過尋找數(shù)學函數(shù)表達式的最小值問題,來展示這三種算法搜尋最優(yōu)解的效率。

優(yōu)化問題:

min f(x)=100*(x2-x1^2)^2+10*(x1-1)^2

s.t. x1^2+x2^2=<9.0

isight優(yōu)化步驟:

1、構建優(yōu)化流程,application組件采用calculator,process 組件選用optimization;

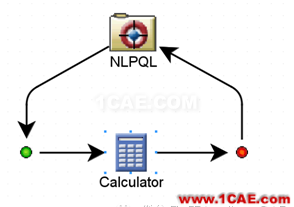
圖1-優(yōu)化流程構建

2、設置優(yōu)化算法、設計變量、約束及目標,設計變量初始值為x1=2.0,x2=3.0;

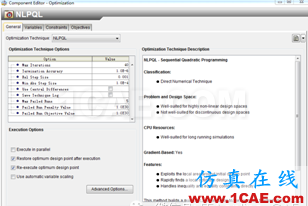
圖2-優(yōu)化算法及參數(shù)設置

3、查看優(yōu)化結果,并比較3種梯度算法搜尋全局最優(yōu)解的效率。

圖3-三種優(yōu)化算法的迭代歷史

圖 3給出了三種算法的搜尋歷程,算法收斂準則均設置為1.0e-6,設計空間為以(0,0)為圓心半徑為3.0的圓域內(nèi),初始點為(2.0,3.0)不在設計空間內(nèi)部,NLPQL算法迭代27次能搜尋到全局最優(yōu)解(0.986,0.975),LSGRG算法迭代10次找到局部最優(yōu)解 (1.590,2.544),這個局部解剛好在設計區(qū)域的邊界上,因為LSGRG算法的搜尋梯度和它的臨界約束相關,MMFD算法迭代8次找到局部解 (1.523,2.342),這個點剛好滿足目標函數(shù)高階項接近零。以上結果可以發(fā)現(xiàn),初始點不在設計區(qū)域內(nèi),NLPQL算法通過多次迭代能搜尋到全局最優(yōu)解,而LSGRG和MMFD算法能用較少的迭代次數(shù)搜尋到一個局部最優(yōu)解而完成迭代過程。

下面考察3種算法在無約束情況下搜尋最優(yōu)解的效率,去掉設計區(qū)域在圓域內(nèi)的限制,設計空間改為無限平面域,初始點位置不變,從圖4中可以看出NLPQL和LSGRG算法都能搜尋到全局最優(yōu)解,而MMFD算法依然在一個局部最優(yōu)解處停止搜尋,從迭代歷程上看NLPQL算法和LSGRG算法相比能以更少的迭代次數(shù)獲得全局最優(yōu)解。

本文以數(shù)學函數(shù)表達式為例對比了isight中3中梯度算法的效率,在有約束情況下 NLPQL能搜尋到全局最優(yōu)解,而LSGRG和MMFD 算法只能搜尋到局部解;在無約束情況下,NLPQL比LSGRG算法能更快速搜尋到全局最優(yōu)解

開放分享：優(yōu)質(zhì)有限元技術文章,助你自學成才